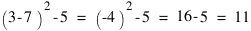Taschenrechner mit seltsamen Rechenwegen...
1,
2,
3Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » So 30. Nov 2014, 18:48
Hi,
ich habe mit meinem Sohn Mathe geübt und etwas seltsames an seinem Sharp-Taschenrechner beobachtet:

- P1090821.JPG (77.75 KiB) 4855-mal betrachtet
Nach meinen bescheidenen Rechenkünsten sollte da -11 herauskommen.
Der ATARI bestätigt dies:
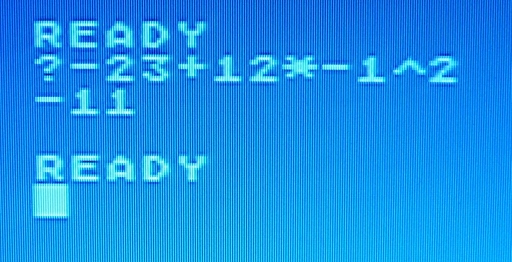
- P1090827.JPG (90 KiB) 4855-mal betrachtet
Die selbe Rechnung in meinen alten Casio-Rechner eingegeben liefert auch das korrekte Ergebnis.
Da ich mal davon ausgehe dass ich von Hand das korrekte Ergebnis ausgerechnet habe, was ist denn bei der Eingabe in den Sharp falsch?
Ich könnte ihm jetzt den ATARI mit in die Schule geben; aber ich trenne mich nur ungern von meinem Rechenknecht...

Sleeπ
Re: Taschenrechner mit seltsamen Rechenwegen...
von Count » So 30. Nov 2014, 19:10
Der Sharp rechnet -(1²) statt (-1)².
Re: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » So 30. Nov 2014, 19:51
Ja, das stimmt - bin ich inzwischen auch drauf gekommen.

Aber was soll das? Ich habe das Minuszeichen der "-1" mit der "+/-"-Taste eingegeben, womit dem Rechner doch klar sein sollte dass das "-" zu der Zahl gehört. Alle anderen (Taschen-) Rechner im Hause, die ich inzwischen ausprobiert habe (inkl. der Rechner von OS X, XP & Win7), rechnen bei der obigen Eingabe das korrekte Ergebnis aus -
ohne noch zusätzliche Klammern setzen zu müssen (die man auch nicht schreiben würde).
Das führt die beworbene WriteView-Funktionalität ja etwas ad absurdum:
"
Die neuen, bunten WriteView TM Schulrechner von Sharp zeigen die eingegebenen Formeln im Display genau so an, wie der Schüler die Darstellung aus dem Mathematikbuch kennt."
QuelleWenn ich die Formel eingebe, wie sie auf dem Papier steht, kommt das falsche Ergebnis raus.
Ich gebe das Ding, wenn noch möglich, zurück und hole ihm einen Rechner der die Aufgabe
ohne rumtrickserei richtig löst. Wenn man bei dem Stress in einer Arbeit noch auf so was achten muss und sich dann Fehler einbaut - das muss ja nicht sein.
Ganz nebenbei ist mir auch noch aufgefallen dass man die Beschriftung auf dem Hochglanz-Gehäuse je nach Lichteinfall gar nicht oder nur schwer lesen kann - bei Stress auch nicht gerade hilfreich.
Mal sehen wie die aktuellen Casios mit "natural v.p.a.m." sich da schlagen.
Sleeπ
Re: Taschenrechner mit seltsamen Rechenwegen...
von 8bitjunkie » So 30. Nov 2014, 23:12
lach... Fast so schön wie das falsch rechnende Excel

Re: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » Mo 1. Dez 2014, 08:10
Sleepy hat geschrieben:Mal sehen wie die aktuellen Casios mit "natural v.p.a.m." sich da schlagen.
Ich habe gerade mal zwei Casios von unserem Azubi getestet, beide mit "natürlicher Dartstellung", die verhalten sich genau so...

Sleepy
Re: Taschenrechner mit seltsamen Rechenwegen...
von dl7ukk » Mo 1. Dez 2014, 09:18
Hi,
ist das wirklich ein Fehler? Oder liegt es einfach an der
Notationj?
Das sollte in der mickrigen Anleitung des Rechenknechtes stehen. (Die sich leider oft nicht ohne Laborausrüstung lesen lässt.)
Re: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » Mo 1. Dez 2014, 09:49
Da es sich bei verschiedene Hersteller so verhält, scheint es tatsächlich so gewollt zu sein...
Zitat aus dem verlinkten Wiki-Eintrag:
"Direkte algebraische Logik – wird je nach Hersteller mit „D.A.L.“ oder „V.P.A.M.“ – engl. für Visually Perfect Algebraic Method – bezeichnet und ist in der Regel auf dem Gehäuse aufgedruckt:
- Rechner mit dieser Eingabemethode zeigen in einer alphanumerischen Zeile die Eingabe an,
auch Funktionen werden so eingegeben, wie man sie auch schreibt."
Wenn ich die Rechnung "-1^2" so eingebe wie ich sie schreibe ist das Ergebnis
falsch.
Andersherum käme ich nicht auf die Idee die "-1"
bei der Eingabe in den Rechner noch mal
extra zu klammern. Das ist für mich nicht praxistauglich. Unserem Azubi war dieser Umstand auch nicht bekannt - und er benutzt einen gerade getesteten Casio schon ein paar Jahre... .
Ich werde mal - mit Hilfe der angedeuteten Lupe

- das Anleitungsposter studieren. Über einen Hinweis dass man extra Klammern muss bin ich bisher nicht gestolpert. Dafür kann man Klammern weglassen - z.B. am Ende eines Ausdruckes vor dem Gleichheitszeichen.

Sleepy
Re: Taschenrechner mit seltsamen Rechenwegen...
von Speak » Mo 1. Dez 2014, 11:44
Mein Sharp kommt auch auf -35.
Egal - ich hätte auf jeden Fall Klammern gesetzt, auch nur um dem Dilemma (Vorzeichen oder Minus) aus dem Weg zu gehen.
-1^2 --> -(1*1) --> -1
(-1)^2--> (-1)*(-1) --> 1
... und mit dem Sharp kontrolliert.
BG Speak
Wertigkeit siehe auch hierRe: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » Mo 1. Dez 2014, 12:39
Die Regel (wenn es sie denn gibt) dass man die zu quadrierende Zahl, wenn sie ein negatives Vorzeichen hat, klammern muss, war mir bis dato jedenfalls unbekannt.
Aus dem verlinkten Artikel würde ich das immer noch nicht als Regel herauslesen; bei dem unter PoKlaPS gegebene Beispiel
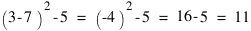
- fetch.png (655 Bytes) 4778-mal betrachtet
hätte ich nach dem Auflösen der Klammer (3-7) die Klammer um die -4 weglassen und -4^2-5 geschrieben.
Ich werde mich heute Abend mal mit dem Mathe-Lehrer in Verbindung setzen ob ihm diese Eigenheit der Rechner bekannt ist (was ich ja mal schwer hoffe). Bis zu meinem Sohn war es jedenfalls noch nicht vorgedrungen.
Mich wundert halt das anscheinend gerade
die Rechner, die damit beworben werden dass man die Formel genau wie im Buch abgebildet eingeben kann, diese imho eher unübliche Syntax verlangen.
Sleepy
Re: Taschenrechner mit seltsamen Rechenwegen...
von dl7ukk » Mo 1. Dez 2014, 16:22
Hallo Sleepy,
Du kannst Deinen Taschenrechner wieder lieb haben, er macht nur was er soll. Eine Erklärung habe ich der Hilfe zum Gnome-Taschenrechner gefunden.
- Code: Alles auswählen
Potenzen und Wurzeln
Potenzen können eingegeben werden, indem Sie eine hochgestellte Zahl hinter den Wert setzen.
5²
Der Kehrwert einer Zahl wird mit dem Kehrwertsymbol ⁻¹ (Strg+I) eingegeben.
3⁻¹
Potenzen können auch mit dem ^-Symbol berechnet werden. Dadurch wird eine Potenz zur Gleichung.
5^(6−2)
Es macht eben einen Unterschied ob eine Potenz direkt --also mit hochgestellter Zahl-- oder als Gleichung berechnet wird.
Ich, als mathematisches Embryo, finde das sehr spitz, aber es ist wohl so. Was Win* und der ATARI machen steht auf einem anderen Blatt.
Re: Taschenrechner mit seltsamen Rechenwegen...
von FlorianD » Mo 1. Dez 2014, 16:40
das hat was damit zu tun, in welcher Reihenfolge (mit welcher Priorität) die Rechenzeichen abgearbeitet werden. Normalerweise in dieser Reihenfolge (absteigende Priorität):
(), Wurzeln/Potenzen, * und :, + und -
7-2^2 wird so gerechnet:
2^2=4
dann
7-4=3
würde man stur von links nach rechts rechnen (was aber falsch ist, denn wir wissen aus dem Matheunterricht, dass ^2 zuerst gerechnet wird):
7-2=5
5^2=25
oder rechnet wirklich jemand so 7-2^2=25 ? (FALSCH!!!)
siehe auch
http://de.wikipedia.org/wiki/Liste_von_ ... MathematikRe: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » Di 2. Dez 2014, 07:38
dl7ukk hat geschrieben:Es macht eben einen Unterschied ob eine Potenz direkt --also mit hochgestellter Zahl-- oder als Gleichung berechnet wird.
Mir ging es jetzt mehr um die Basis. Wenn´s so eingegeben werden muss dann ist es halt so; anscheinend ist es bei den aktuellen, halbwegs besseren Taschenrechnern inzwischen ja so üblich.
Aber ich gebe mich geschlagen; dann muss ich mich halt umgewöhnen oder auf die schicke Anzeige von Brüchen verzichten und meinen alten FX-115 weiternutzen.

Ich finde es halt nach wie vor eigenartig, da ich, wie oben beschrieben, das Vorzeichen der Zahl mit einer extra Taste eingeben
muss (Sprich: das Vorzeichen ist
nicht identisch mit dem Rechenzeichen und wird im Display auch
anders dargestellt) wodurch ja eigentlich klar sein dürfte dass das "-" zur Zahl gehört und kein Rechenzeichen ist was wg. "Potenz vor Punkt vor Strich" erst zum Schluss berücksichtigt wird.
Anders wäre es natürlich wenn die Basis ein Term ist.
In Florian´s "7-2^2" ist klar daß es sich um ein Rechenzeichen handelt.
Bei "7*-2^2" wäre (mir) aber auch genau so klar dass das "-" zur "2" gehört.

Aber ich ich werde das Sharp-Modell trotzdem durch einen Casio ersetzen; der Sharp hat eine Klavierlack-Optik die, je nach Beleuchtungssituation, ziemlich schlecht abzulesen ist. Die Casios, die ich mir jetzt testweise angesehen habe, haben eine besser ablesbare, matte Oberfläche.
Ich danke für die Erleuchtung,
Sleepy
Re: Taschenrechner mit seltsamen Rechenwegen...
von Bunsen » Di 2. Dez 2014, 20:11
- Zwei Operatoren hintereinander gibt es nicht ohne Klammern ( bei Taschenrechnern und alten Computern gelten anscheinend andere Regeln)
- "-2^2=-4" aber "(-2)^2=4"
Florian hat das sehr gut erklärt.
Re: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » Di 2. Dez 2014, 20:30
Bunsen hat geschrieben:...und alten Computern gelten anscheinend andere Regeln)
Selbst mein oller Windows 7-Laptop schluckt die falsche Syntax anstandslos...

Ich habe in diesem Zusammenhang auch mehrere Internetseiten über Potenzrechnung besucht; selbst Potenz-Rechner auf diesen Seiten rechnen teilweise mit der falschen Syntax...

Ich werde mir (und meinem Filius) das korrekte Klammern angewöhnen; über ihn bin ich erst darüber gestolpert nachdem ich ihn beim Matheüben nahegelegt habe das Ergebnis das gelöste Gleichungssystemes durch einsetzen zu überprüfen und er - trotz korrektem Ergebnis - nach mehrmaligen hin- und hertippen im Taschenrechner meinte das es falsch wäre...
Sleeπ
Re: Taschenrechner mit seltsamen Rechenwegen...
von Wizard » Mi 3. Dez 2014, 10:20
Der Casio meines Azubis kann das auch nicht.
 Casio_.JPG
Casio_.JPGRe: Taschenrechner mit seltsamen Rechenwegen...
von eda70 » Mi 3. Dez 2014, 10:45
Ich finde das auch komisch, was der Taschenrechner da macht.
Das Minus gehört zur Zahl ist damit -in meinen Augen- kein Rechenzeichen, auf das die Wertigkeit der Rechenoperationen Anwendung findet. Sonst müsste man ja immer alle negativen Zahlen klammern...
Was hat denn der Mathe-Lehrer gesagt?
Re: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » Mi 3. Dez 2014, 10:53
Noch nichts; ich hatte gehofft ihn gestern Abend bei einem Berufs-Beratungsabend in der Schule zu treffen und wollte ihn dann nicht abends telefonisch belästigen.
Leider war er nicht da - da muss ich heute Abend doch zum Hörer greifen...

Sleepy
Re: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » Mi 3. Dez 2014, 18:58
Ich habe gerade mit dem Mathe-Lehrer telefoniert: Er kannte diese Eigenheit auch nicht; seine Taschenrechner rechnen auch ohne extra Klammer korrekt. Er würde Ausdrücke wie -1^2 auch nicht mit einer Klammer schreiben.
Er will die Problematik aber im Unterricht ansprechen.

Ich habe mir die sehr übersichtlich gestaltete Anleitung zu unserem Sharp inzwischen mal angesehen; einen direkten Hinweis darauf dass man eine negative Basis in Klammern setzen muss habe ich nicht gefunden; oder ich habe den Hinweis nicht erkannt.

Evt. steht´s hier mit drin:

- sharp.tiff (112.5 KiB) 4634-mal betrachtet
Ich sehe es aber nicht...
Sleeπ
Re: Taschenrechner mit seltsamen Rechenwegen...
von HiassofT » Mi 3. Dez 2014, 21:17
Ich hatte auf der Uni ziemlich viel Mathematik und mein erster Gedanke war: Die Angabe ist Blödsinn, da fehlen die Klammern, in der Form ist sie kein korrekter Ausdruck.
Hab' dann mit meiner Schwester telefoniert (die ist Mathe-Lehrerin) und die sagt auch: Blödsinn, ohne die Klammern ist nicht eindeutig was gemeint ist.
Eine Faustregel ist: es dürfen nie 2 Rechenzeichen (+, -, *, /) hintereinander kommen.
Sie gibt ihren Schülern gern folgendes Beispiel: was wäre denn das Ergebnis von 2x+-/7? Einige tippen dann ohne nachzudenken drauf los in den Taschenrechner und verstehen dabei nicht, daß daß das gar kein gültiger Ausdruck war :)
Mit den Taschenrechnern ist das so eine Sache, zum Teil fressen sie ungültige Eingaben, verschiedene Hersteller geben aber verschiedene Ergebnisse aus.
Selbst wenn man das spezielle "Vorzeichen-Minus" am Taschenrechner nimmt ist es leider nicht eindeutig was mit "-1^2" gemeint ist: (-1)^2 oder -(1^2). Das Vorzeichen-Minus sagt, daß die Zahl die danach kommt negativ ist. Wenn danach aber keine Zahl sondern ein "Rechenschritt" (1^2) kommt, wirds schwierig - einerseits könnte man sagen, daß das ^2 stärker bindet als +/-, andererseits könnte man sagen, daß sich das Vorzeichen-Minus nur auf eine Zahl beziehen soll.
Unklare Sachen möchte man in der Mathematik nicht haben, deshalb vermeidet man sie und verwendet Klammern, damit ist dann eindeutig klar was gemeint ist.
Achja: solche Beispiele eignen sich ziemlich gut um zu erklären wieso man sich nicht blind auf das Ergebnis aus dem Taschenrechner/Computer verlassen soll. Vielleicht war ja genau das die Intention des Lehrers bei dem Beispiel.
so long,
Hias
Re: Taschenrechner mit seltsamen Rechenwegen...
von Sleepy » Do 4. Dez 2014, 07:32
Die ursprüngliche Aufgabe lautete:
(6b-5)(2b+3)=-23+12b^2
Die "-1" war das Ergebnis der Gleichung, eingesetzt in den rechten Term.
HiassofT hat geschrieben:Sie gibt ihren Schülern gern folgendes Beispiel: was wäre denn das Ergebnis von 2x+-/7?
Dass so etwas Quatsch ist ist klar; es ging mir einzig um Zahlen mit negativem Vorzeichen.

Sleepy
1,
2,
3